Over all the blog posts this will be the last one for the semester. So to wrap up all the blogs I’ve decided to end it all with something that threw me off on the last exam we took. It was a simple find the derivative problem but the appearance of it was daunting so I messed up. I’ll do a related example of the problem.
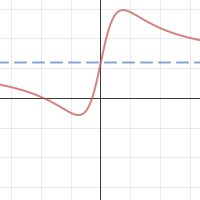
Find the derivative of
First we must remember the basic rules when it comes to dealing with derivatives of fractions.
so we find b, b’, t, and t’ and plug them into the equation
and
and
Now to plug them into the equation…
Now we work it out…
Now we simplify by removing parts that cancel each other out and we get our answer…
I hope this will help people avoid any minor issues that derivatives may cause.


You must be logged in to post a comment.